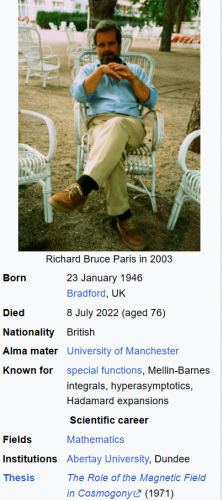
Le 8 juillet dernier 2022 le mathématicien Richard Bruce Paris, mon oncle, nous quittait dans le plus grand silence. Ce blog fut plusieurs mois durant l'unique lien informationnel.
En novembre, plusieurs éminents scientifiques, ses collègues et contacts ont pris contact pour information, choqués d'apprendre cette brutale disparition.
Ils ont créé sa page wiki qui manquait.
https://en.wikipedia.org/wiki/Richard_Bruce_Paris
"Le travail de R. Paris traite du comportement asymptotique d’un large éventail de fonctions spéciales, dans de nombreux cas avec un lien avec des problèmes physiques.
En collaboration avec David Kaminski, professeur agrégé de mathématiques à l’Université de Lethbridge, Paris a publié la monographie Asymptotics et Mellin-Barnes integrals. C’est l’un des rares manuels qui traite de manière approfondie de l’application des transformations de Mellin, en particulier à différents problèmes asymptotiques. Les intégrales de Mellin-Barnes constituent une classe spéciale d’intégrales de contour qui comportent des fonctions spéciales dans l’intégrande, le plus souvent des produits de fonctions gamma. Leur évaluation repose sur le théorème du résidu et nécessite des manipulations appropriées du chemin d’intégration. Le nom est dû aux mathématiciens R. H. Mellin et E. W. Barnes. De nombreuses intégrales peuvent être transformées en une représentation de Mellin-Barnes, en écrivant leurs entiers en termes de transformées de Mellin inverses. Dans le contexte des intégrales de type Laplace, cette technique offre une alternative puissante à la méthode de Laplace. En général, cependant, il admet une applicabilité plus large et beaucoup de place pour les modifications. Cette polyvalence est démontrée au moyen de plusieurs exemples de la théorie des nombres et des intégrales de dimension supérieure. [5]
Dans sa monographie Hadamard Expansions and Hyperasymptotic Evaluation: An Extension of the Method of Steepest Descent, au moyen d’exemples théoriques et numériques, Paris illustre l’application de la méthode de Laplace et les possibilités d’atteindre une plus grande précision. Le terme expansions de Hadamard décrit un type particulier d’expansions asymptotiques dont les coefficients sont à nouveau des séries. Il fait référence au mathématicien français Jacques Hadamard qui a introduit la première série de ce type en 1908 dans son article Sur l’expression asymptotique de la fonction de Bessel. [6]
Paris a également organisé les chapitres 8 et 11, respectivement sur le Gamma incomplet et sur les fonctions de Struve et les fonctions connexes, de la Bibliothèque numérique des fonctions mathématiques du NIST et du Manuel des fonctions mathématiques du NIST. Il a validé la version originale en 2010 et a été rédacteur en chef adjoint de ses chapitres de 2015 jusqu’à sa mort. "
Hommage à Richard Bruce Paris, mathématicien - Le Blog de Sylvie Neidinger (blogspirit.com)
Sylvie Neidinger